American Roulette Odds (Over 100 Roulette Probabilities)

Last update: 27 mins Arved Klöhn Arved Klöhn

This page lists all important American Roulette Odds and Probabilities. We list all basic probabilities for American Roulette and dozens of combined and long-term American Roulette odds – for example betting on colors multiple times in a row, vs. betting on single numbers.

If you’re missing any probability, please let us know below via a comment below!

American Roulette 17
American Roulette Probabilities

American Roulette: Basic Odds, Probabilities and Payouts

First of all, here are the odds, probabilities and payouts for all basic bets that can be placed when playing American Roulette:

American Roulette: Basic Odds and Probabilities

BetWins onOddsPayout
Straight UpSingle number2.63%
(1 : 37.0)		35 : 1
SplitAny two adjoining numbers5.26%
(1 : 18.0)		17 : 1
StreetAny three horizontal numbers7.89%
(1 : 11.7)		11 : 1
CornerAny four adjoining numbers10.53%
(1 : 8.5)		8 : 1
Double StreetAny six numbers from two horizontal rows15.79%
(1 : 5.3)		5 : 1
1st column1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 3431.58%
(1 : 2.2)		2 : 1
2nd column2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 3531.58%
(1 : 2.2)		2 : 1
3rd column3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 3631.58%
(1 : 2.2)		2 : 1
1st dozen1 – 1231.58%
(1 : 2.2)		2 : 1
2nd dozen13 – 2431.58%
(1 : 2.2)		2 : 1
3rd dozen25 – 3631.58%
(1 : 2.2)		2 : 1
EvenAny even number47.37%
(1 : 1.1)		1 : 1
OddAny odd number47.37%
(1 : 1.1)		1 : 1
RedAny red number47.37%
(1 : 1.1)		1 : 1
BlackAny black number47.37%
(1 : 1.1)		1 : 1
1st half1 – 1847.37%
(1 : 1.1)		1 : 1
2nd half19 – 3647.37%
(1 : 1.1)		1 : 1
American Roulette: Basic Odds and Probabilities

Expected Value and House Edge for American Roulette

Expected Value for American Roulette

Roulette has a simple house edge. The payouts for all bets are slightly lower than the odds. For example, the odds of hitting a specific number, say 17, are 1:37, but the payout is only 35:1.

For all bets, the House Edge in American Roulette is 5.26%.

This means the average return on any bet is 94.74%.

A simple example: Say you bet $100 on red. The probability of the wheel landing on red is \frac{18}{38} (there are 18 red numbers and 38 numbers in total). If the wheel lands on red you receive $200 (your initial bet back plus the winnings). If the wheel lands on any other color (black or green zero), you receive nothing. Thus on average, you receive

    \[\frac{18}{38}\times\$200 = \$94.74\]

For all bets in American Roulette, you can run a similar calculation and it will show the same result – every bet has an expected return of 94.74% of the investment.

Roulette Bonus Will Impact Your Winning Chances

While the odds per spin do not change, using a roulette bonus will impact your odds of winning and losing in the long term. Bonuses work as a safety net and generally activate after you have lost your real money. You will then have a chance to use this bonus to continue to play. Once you have met the bonus requirements, you can withdraw your winnings and thus have the opportunity to walk away with something rather than nothing.

It is important to be aware that most bonuses are not optimal for roulette players. The majority of online casino bonuses come with wagering requirements. This means you must wager your bonus a certain number of times before it will be converted to real currency. The issue is that, given the low house edge on roulette games, you are often excluded from playing with your bonus at any of the casinos’ roulette tables. Alternatively, any roulette gameplay will not be counted, or it will count very little toward the wagering requirement.

This is why looking for actual roulette bonuses is important so that you can keep playing roulette with your bonus funds. The easiest way to find them is to use casino comparison sites, such as KingCasinoBonus, Gamblizard, and Bojoko. The latter is convenient, as Bojoko has not only created a list dedicated to roulette bonuses, but you can filter it down to remove pesky terms and conditions.

Roulette bonuses reduce the house edge, as you have a way to win money after your real funds have run out, and it is, therefore, recommended to get this safety net in place whenever possible.

Long-term Odds

Roulette is a game that is usually played over more than one spin of the wheel. The probabilities of the game shift when playing multiple spins. For example, it’s rather unlikely (1:37) to hit the number 17 in one spin. But if you spin the wheel 26 times, the odds of having the number 17 at least once are virtually even. The following table shows a few of the long-term odds and probabilities for American Roulette.

Long-term Odds and Probabilities (American Roulette)

The following table shows the odds and probabilities of repeated occurrences of the same event in American Roulette:

Thing to happenProbabilityFormula
Hitting the same color
The same color (e.g. red) over 2 spins22.44%
(1 : 3)

    \[\left(\frac{18}{38}\right)^2\]

The same color (e.g. red) over 3 spins10.63%
(1 : 8)

    \[\left(\frac{18}{38}\right)^3\]

The same color (e.g. red) over 4 spins5.03%
(1 : 19)

    \[\left(\frac{18}{38}\right)^4\]

The same color (e.g. red) over 5 spins2.38%
(1 : 41)

    \[\left(\frac{18}{38}\right)^5\]

The same color (e.g. red) over 10 spins0.06%
(1 : 1,757)

    \[\left(\frac{18}{38}\right)^{10}\]

Hitting the same number
The same number (e.g. 17) over 2 spins0.07%
(1 : 1,443)

    \[\left(\frac{1}{38}\right)^2\]

The same number (e.g. 17) over 3 spins0.002%
(1 : 54,871)

    \[\left(\frac{1}{38}\right)^3\]

The same number (e.g. 17) over 4 spins0.00005%
(1 : 2,085,135)

    \[\left(\frac{1}{38}\right)^4\]

Not hitting 0 or 00
Neither 0 or 00 over 1 spin94.74%
(18.0 : 1)

    \[\frac{36}{38}\]

Neither 0 or 00 over 5 spins76.31%
(3.2 : 1)

    \[\left(\frac{36}{38}\right)^5\]

Neither 0 or 00 over 13 spins49.52%
(1 : 1)

    \[\left(\frac{36}{38}\right)^13\]

Neither 0 or 00 over 20 spins33.91%
(1 : 2)

    \[\left(\frac{36}{38}\right)^{20}\]

Neither 0 or 00 over 100 spins0.45%
(1 : 222)

    \[\left(\frac{36}{38}\right)^{100}\]

Neither 0 or 00 over 200 spins0.002%
(1 : 49,683)

    \[\left(\frac{36}{38}\right)^{200}\]

Not hitting a specific number
No 17 (or any other single number) over 5 spins76.31%
(3.2 : 1)

    \[\left(\frac{37}{38}\right)^5\]

No 17 (or any other single number) over 20 spins58.66%
(1.4 : 1)

    \[\left(\frac{37}{38}\right)^{20}\]

No 17 (or any other single number) over 26 spins49.99%
(1 : 1)

    \[\left(\frac{37}{38}\right)^{26}\]

No 17 (or any other single number) over 100 spins6.95%
(1 : 13)

    \[\left(\frac{37}{38}\right)^{100}\]

No 17 (or any other single number) over 200 spins0.48%
(1 : 206)

    \[\left(\frac{37}{38}\right)^{200}\]

No 17 (or any other single number) over 500 spins0.0002%
(1 : 617,925)

    \[\left(\frac{37}{38}\right)^{500}\]

American Roulette: Long term probabilities

Odds Betting on 1:1 Chances

Let’s take a look at what happens when you bet on even chances (red or black, odd or even, 1st or 2nd half) multiple times in a row when playing American Roulette. The following tables show the probability of winning or losing a certain amount of money.

Betting on Even Chances 5 Times

If you bet $100 on even chances in American Roulette 5 times the probability of winning more bets than losing is slightly over 45%. Those are the exact probabilities:

ResultProbabilityFormula
Win 5 times
(win $500)		2.38%
(1 : 41)

    \[\left(\frac{18}{38}\right)^{5}\]

Win 4 times or more
(win $300+)		15.63%
(1 : 5.4)

    \[\sum_{k=4}^5 \binom{k}{5} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{5-k}\]

Win 3 times or more
(win $100+)		45.07%
(1 : 1.2)

    \[\sum_{k=3}^5 \binom{k}{5} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{5-k}\]

Win 2 times or less
(lose $100+)		54.93%
(1.2 : 1)

    \[\sum_{k=0}^2 \binom{k}{5} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{5-k}\]

Win 1 time or less
(lose $300+)		22.21%
(1 : 3.5)

    \[\sum_{k=0}^1 \binom{k}{5} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{5-k}\]

Win 0 times
(lose $500)		4.04%
(1 : 24)

    \[\left(\frac{20}{38}\right)^{5}\]

American Roulette: Betting on even chances 5 times

Betting on Even Chances 20 Times

If you bet $100 on even chances in American Roulette 20 times the probability of winning more bets than losing is only 32%. Those are the exact probabilities:

ResultProbabilityFormula
Win 20 times
(win $2,000)		0.00003%
(1 : 3,091,873)

    \[\left(\frac{18}{38}\right)^{20}\]

Win 15 times or more
(win $1,000+)		1.15%
(1 : 86)

    \[\sum_{k=15}^20 \binom{k}{20} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{20-k}\]

Win 13 times or more
(win $600+)		8.75%
(1 : 10)

    \[\sum_{k=13}^20 \binom{k}{20} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{20-k}\]

Win 11 times or more
(win $200+)		32.23%
(1 : 2)

    \[\sum_{k=11}^20 \binom{k}{20} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{20-k}\]

Break even exactly17.14%
(1 : 5)

    \[\binom{10}{20} \left(\frac{18}{38}\right)^{10} \left(\frac{20}{38}\right)^{10}\]

Win 9 times or less
(lose $200+)		50.63%
(1 : 1)

    \[\sum_{k=0}^9 \binom{k}{20} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{20-k}\]

Win 7 times or less
(lose $600+)		18.89%
(1 : 4)

    \[\sum_{k=0}^7 \binom{k}{20} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{20-k}\]

Win 5 times or less
(lose $1,000+)		3.55%
(1 : 27)

    \[\sum_{k=0}^5 \binom{k}{20} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{20-k}\]

Win 0 times
(lose $2,000)		0.0003%
(1 : 375,899)

    \[\left(\frac{20}{38}\right)^{20}\]

American Roulette: Betting on even chances 5 times

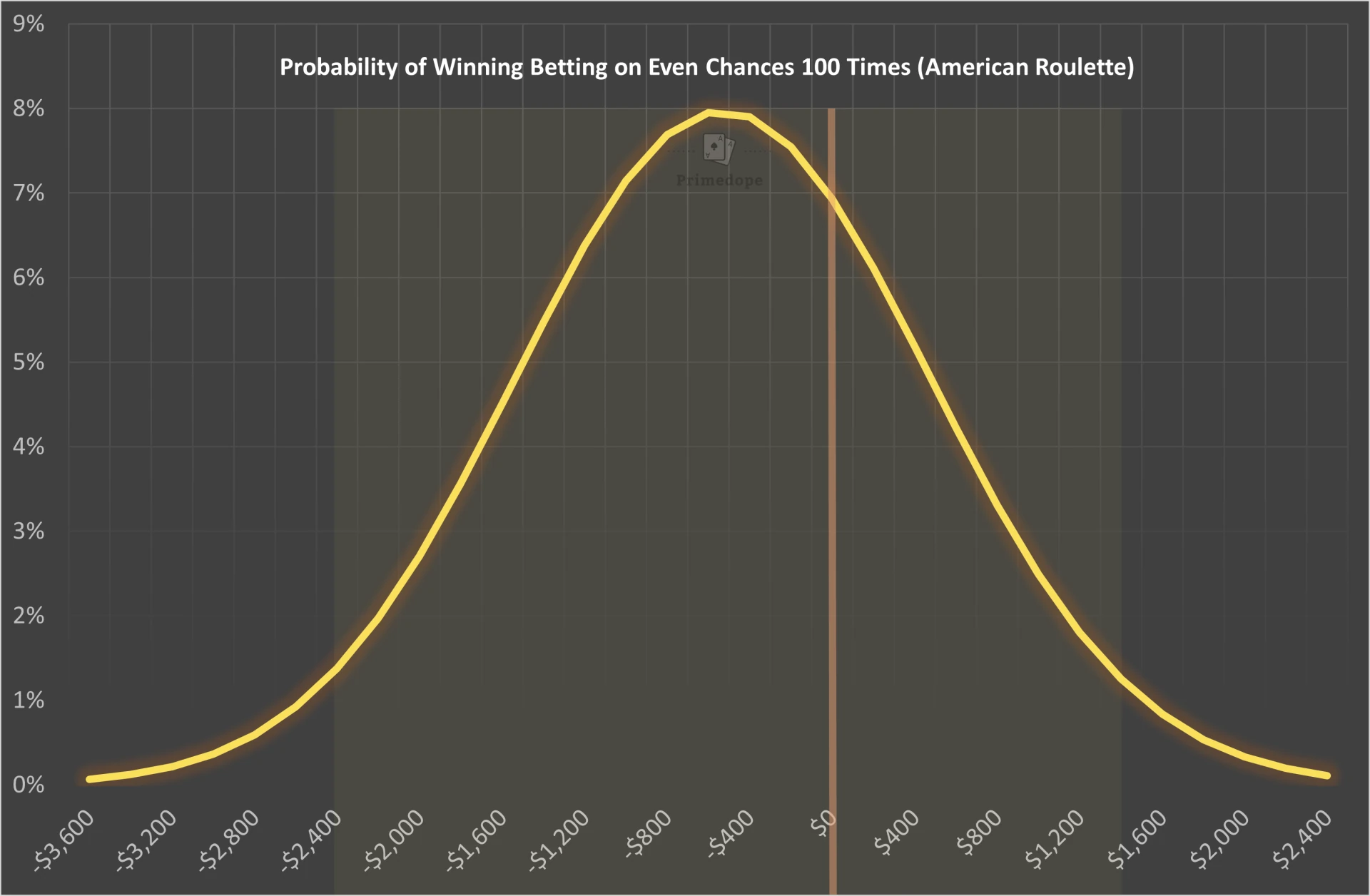
Betting on Even Chances 100 Times

If you bet $100 on even chances in American Roulette 100 times the probability of winning more bets than losing is only 26.5%. Those are the exact probabilities:

ResultProbabilityFormula
Win 70 times or more
(win $4,000+)		0.0004%
(1 : 256,765)

    \[\sum_{k=70}^{100} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

Win 60 times or more
(win $2,000+)		0.75%
(1 : 132)

    \[\sum_{k=60}^{100} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

Win 55 times or more
(win $1,000+)		7.67%
(1 : 12)

    \[\sum_{k=55}^{100} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

Win 51 times or more
(win $200+)		26.50%
(1 : 3)

    \[\sum_{k=51}^{100} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

Break even exactly6.93%
(1 : 13)

    \[\binom{50}{100} \left(\frac{18}{38}\right)^{50} \left(\frac{20}{38}\right)^{50}\]

Win 49 times or less
(lose $200+)		66.57%
(2.0 : 1)

    \[\sum_{k=0}^{49} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

Win 45 times or less
(lose $1,000+)		35.48%
(1 : 2)

    \[\sum_{k=0}^{45} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

Win 40 times or less
(lose $2,000+)		8.41%
(1 : 11)

    \[\sum_{k=0}^{40} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

Win 30 times or less
(lose $4,000+)		0.03%
(1 : 3,298)

    \[\sum_{k=0}^{30} \binom{k}{100} \left(\frac{18}{38}\right)^k \left(\frac{20}{38}\right)^{100-k}\]

American Roulette: Betting on even chances 100 times

The following graph shows the probability distribution when betting $100 on even chances over 100 spins. The orange line is the break-even point (win 50 bets, lose 50 bets) and the highlighted area is the range of results where you will end up 95% of the time.

Probability distribution when betting on even chances 100 times (American Roulette)
Probability distribution when betting on even chances 100 times (American Roulette)
(orange line: break even; highlighted area: 95% of all runs will end in this area)

When betting on even chances your chance of winning big amounts of money is very slim. While you don’t risk very much, you also don’t stand to gain a lot as each bet only pays out 1:1.

Let’s see what happens when you bet on events that are less likely but have a higher payout.

Odds Betting on 8:1 Chances

The probabilities when betting on 8:1 chances multiple times a row in American Roulette shift noticeably. 8:1 bets are so-called Corner Bets where you bet on four numbers at the same time. The odds of winning such a bet are 1:8.5 whereas the payout is 8:1.

Betting on 8:1 Chances 5 Times

If you bet $100 on 8:1 chances in American Roulette 5 times, the probability of winning at least once is almost 43%. The maximum loss is only $500 (when you lose all 5 bets), but the potential winnings are much higher than when betting on even chances.

ResultProbabilityFormula
Win at least 4 times
(win $3,100 or more)		0.06%
(1 : 1,778)

    \[\sum_{k=4}^5 \binom{k}{5} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{5-k}\]

Win at least 3 times
(win $2,200 or more)		0.99%
(1 : 100)

    \[\sum_{k=3}^5 \binom{k}{5} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{5-k}\]

Win at least twice
(win $1,300 or more)		8.93%
(1 : 10)

    \[\sum_{k=2}^5 \binom{k}{5} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{5-k}\]

Win at least once
(win $400 or more)		42.66%
(1 : 1.3)

    \[\sum_{k=1}^5 \binom{k}{5} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{5-k}\]

No win
(lose $500)		57.34%
(1.3 : 1)

    \[\left(\frac{34}{38}\right)^{5}\]

American Roulette: Betting on even chances 100 times

Betting on 8:1 Chances 20 Times

If you bet $100 on 8:1 chances in American Roulette 20 times, you need to win at least 3 of those bets to turn a profit. This happens in more than 35% of all cases.

ResultProbabilityFormula
Win at least 6 times
(win $3,400 or more)		1.43%
(1 : 69)

    \[\sum_{k=6}^{20} \binom{k}{20} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{20-k}\]

Win at least 5 times
(win $2,500 or more)		5.21%
(1 : 18)

    \[\sum_{k=5}^{20} \binom{k}{20} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{20-k}\]

Win at least 4 times
(win $1,600 or more)		15.24%
(1 : 6)

    \[\sum_{k=4}^{20} \binom{k}{20} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{20-k}\]

Win at least 3 times
(win $700 or more)		35.32%
(1 : 2)

    \[\sum_{k=3}^{20} \binom{k}{20} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{20-k}\]

Win 2 times or less
(lose $200 or more)		64.68%
(1.8 : 1)

    \[\sum_{k=0}^2 \binom{k}{20} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{20-k}\]

Win 1 times or less
(lose $1,100 or more)		36.25%
(1 : 2)

    \[\sum_{k=0}^1 \binom{k}{20} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{20-k}\]

No win
(lose $2,000)		10.81%
(1 : 8)

    \[\left(\frac{34}{38}\right)^{20}\]

American Roulette: Betting on even chances 100 times

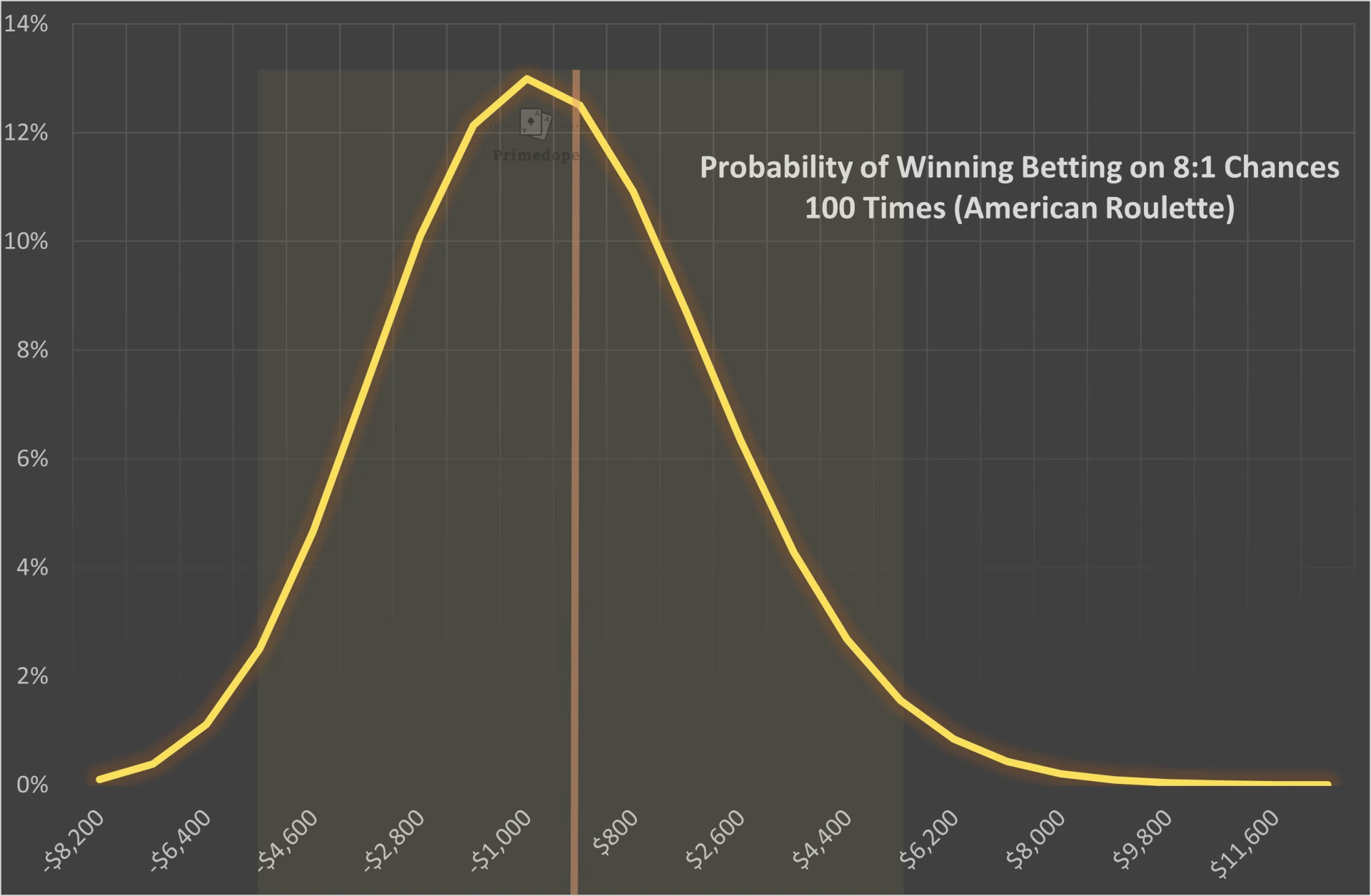
Betting on 8:1 Chances 100 Times

If you bet $100 on 8:1 chances in American Roulette 100 times the probability of turning a profit is 36.11%. Those are the exact probabilities:

ResultProbabilityFormula
Win at least 20 times
(win $8,000 or more)		0.36%
(1 : 278)

    \[\sum_{k=20}^{100} \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win at least 16 times
(win $4,400 or more)		5.87%
(1 : 16)

    \[\sum_{k=16}^{100} \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win at least 14 times
(win $2,600 or more)		16.50%
(1 : 5)

    \[\sum_{k=14}^{100} \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win at least 13 times
(win $1,700 or more)		25.19%
(1 : 3)

    \[\sum_{k=13}^{100} \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win at least 12 times
(win $800 or more)		36.11%
(1 : 2)

    \[\sum_{k=12}^{100} \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win 11 times or less
(lose $100 or more)		63.89%
(1.8 : 1)

    \[\sum_{k=0}^{11} \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win 10 times or less
(lose $1,000 or more)		51.39%
(1 : 1)

    \[\sum_{k=0}^{10} \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win 9 times or less
(lose $1,900 or more)		38.40%
(1 : 2)

    \[\sum_{k=0}^9 \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win 8 times or less
(lose $2,800 or more)		26.26%
(1 : 3)

    \[\sum_{k=0}^8 \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win 6 times or less
(lose $4,600 or more)		8.80%
(1 : 10)

    \[\sum_{k=0}^6 \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

Win 4 times or less
(lose $6,400 or more)		1.62%
(1 : 61)

    \[\sum_{k=0}^4 \binom{k}{100} \left(\frac{4}{38}\right)^k \left(\frac{34}{38}\right)^{100-k}\]

American Roulette: Betting on even chances 100 times

The following graph shows the probability distribution when betting $100 on 8:1 chances over 100 spins. The orange line is the break-even point (win 11 bets, lose 89 bets) and the highlighted area is the range of results where you will end up 95% of the time.

Probability distribution when betting on 8:1 chances 100 times (American Roulette)
Probability distribution when betting on 8:1 chances 100 times (American Roulette)
(orange line: break even; highlighted area: 95% of all runs will end in this area)

When betting on Corners Bets with 8:1 chances, your chance of showing any profit long-term is bigger than when betting on even chances. Also, your chances of winning a significant amount of money are bigger as this bet has a bigger variance. But on the flip side, the chances of losing a lot are also bigger.

Now let’s see what happens when repeating the most volatile roulette bet multiple times:

Odds Betting Straight Up Single Numbers

The probabilities when betting single numbers multiple times a row in American Roulette shift radically. Those bets which you can place on any single number, including the 0 and 00 are called “Straight Up”. The odds of winning such a bet are 1:37 while the payout is 35:1.

Betting on Single Numbers 5 Times

If you bet $100 on single numbers in American Roulette 5 times, the probability of winning at least once is 12.5% and with one win over 5 spins, you stand to win $3,100. The maximum loss is only $500 (when you lose all 5 bets).

ResultProbabilityFormula
Win at least twice
(win $6,700 or more)		0.66%
(1 : 151)

    \[\sum_{k=2}^5 \binom{k}{5} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{5-k}\]

Win at least once
(win $3,100 or more)		12.48%
(1 : 7)

    \[\sum_{k=1}^5 \binom{k}{5} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{5-k}\]

No win
(lose $500)		87.52%
(7 : 1)

    \[\left(\frac{37}{38}\right)^{5}\]

American Roulette: Betting on even chances 100 times

Betting on Single Numbers 20 Times

If you bet $100 on single numbers in American Roulette 20 times, you need to win at only 1 of those bets to turn a profit. This happens in more than 41% of all cases.

ResultProbabilityFormula
Win at least 4 times
(win $12,400 or more)		0.17%
(1 : 602)

    \[\sum_{k=4}^{20} \binom{k}{20} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{20-k}\]

Win at least 3 times
(win $8,800 or more)		1.49%
(1 : 66)

    \[\sum_{k=2}^{20} \binom{k}{20} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{20-k}\]

Win at least twice
(win $5,200 or more)		9.63%
(1 : 9)

    \[\sum_{k=2}^{20} \binom{k}{20} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{20-k}\]

Win at least once
(win $1,600 or more)		41.34%
(1 : 1.4)

    \[\sum_{k=1}^{20} \binom{k}{20} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{20-k}\]

No win
(lose $2,000)		58.66%
(1.4 : 1)

    \[\left(\frac{37}{38}\right)^{20}\]

American Roulette: Betting on even chances 100 times

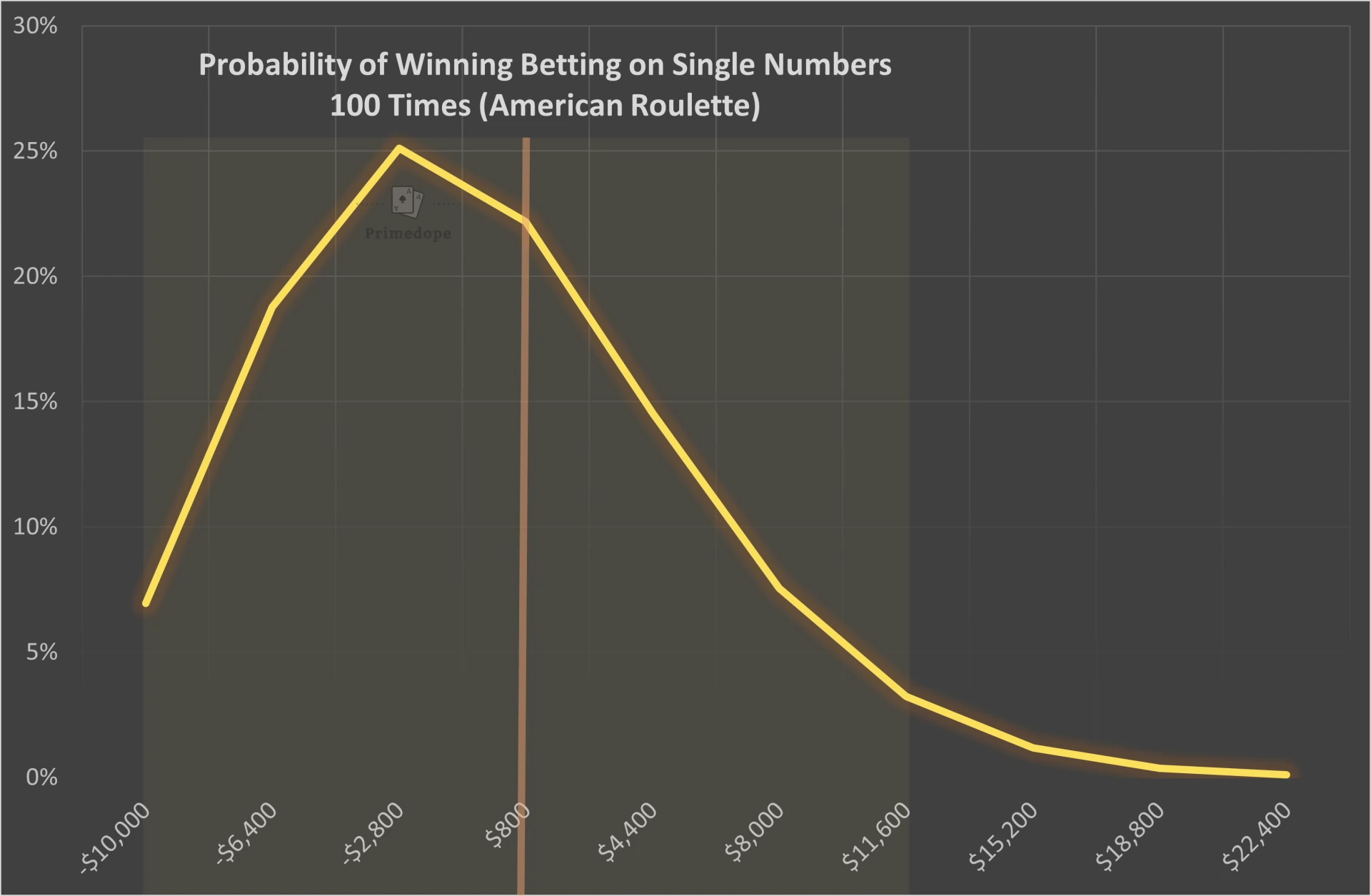
Betting on Single Numbers 100 Times

If you bet $100 on single numbers in American Roulette 100 times the probability of turning a profit is over 49%. Those are the exact probabilities:

ResultProbabilityFormula
Win at least 8 times
(win $18,800 or more)		0.50%
(1 : 198)

    \[\sum_{k=8}^{100} \binom{k}{100} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{100-k}\]

Win at least 6 times
(win $11,600 or more)		4.90%
(1 : 19)

    \[\sum_{k=6}^{100} \binom{k}{100} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{100-k}\]

Win at least 4 times
(win $4,400 or more)		26.98%
(1 : 2.7)

    \[\sum_{k=4}^{100} \binom{k}{100} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{100-k}\]

Win at least 3 times
(win $800 or more)		49.16%
(1 : 1)

    \[\sum_{k=3}^{100} \binom{k}{100} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{100-k}\]

Win 2 times or less
(lose $2,800 or more)		50.84%
(1 : 1)

    \[\sum_{k=0}^2 \binom{k}{100} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{100-k}\]

Win 1 time or no win
(lose $6,400 or more)		25.72%
(1 : 3)

    \[\sum_{k=0}^1 \binom{k}{100} \left(\frac{1}{38}\right)^k \left(\frac{37}{38}\right)^{100-k}\]

No win
(lose $10,000)		6.95%
(1 : 13)

    \[\left(\frac{37}{38}\right)^{100}\]

American Roulette: Betting on even chances 100 times

The following graph shows the probability distribution when betting $100 on single numbers over 100 spins. The orange line is the break-even point (win 3 bets, lose 97 bets) and the highlighted area is the range of results where you will end up 95% of the time.

Probability distribution when betting on single numbers 100 times (American Roulette)
Probability distribution when betting on single numbers 100 times (American Roulette)
(orange line: break even; highlighted area: 95% of all runs will end in this area)

Betting on single numbers is the most volatile bet in American Roulette. This means that both, the chances of winning big and the chances of losing a lot are considerable.

Playing Roulette Online

For those looking to play from the confines of their own home, playing roulette online Canada is an enticing option. The country boasts a vibrant online gaming scene, where players can indulge in various roulette games, from the classic to the more modern variants. The casinos licensed in Canada are renowned for their robust security measures, diverse game selections, and generous bonuses, making Canada an attractive hub for roulette players seeking to experience the thrill of the game from the comfort of their homes.

American Roulette FAQ

What are the best odds in American Roulette?

47.370% or 1 : 1.1

The best odds you can get when playing American Roulette are 1:1.1 or 47.4%. This is the chance of winning any of the even bets (red / black, odd / even, 1st half / 2nd half).

What has the better odds, American or European Roulette?

In general European Roulette has better odds compared to American Roulette. The odds of winning when betting on a single number in European Roulette are 1:36 compared to 1:37 in American Roulette.

What are the odds of hitting red or black in American Roulette?

47.370% or 1 : 1.1

The odds of hitting red in American Roulette are 1:1.1 (47.4%). The odds of hitting black are the same.

What is the most likely color in American Roulette?

Both colors, red and black have the same probability in American Roulette – 47.4%. On average you can expect the ball to land on red a little bit under 50% of the time.

How to win playing American Roulette?

There is no strategy that guarantees a win when playing American Roulette. There isn’t even a strategy that has a positive expectation. But you can increase your chance of winning by placing smart bets.

What are the odds of hitting 0 or 00 in American Roulette?

5.2600% or 1 : 18

The odds of hitting any of the two zeros (0 or 00) in American Roulette are 1:18 or 5.26%. There are 38 numbers in total in American Roulette and 2 of them are zeros. The probability of hitting any of them is 2/38.

What is the most you can win in a single bet in American Roulette?

35 times your bet

If you bet on a single number (Straight Up) in American Roulette you win 35 times your bet if the number wins. For example, if you bet USD20 on the number 17 and it wins, you win USD700.

What are the odds of getting 5 Reds in a row in American Roulette?

2.3800% or 1 : 41

The odds of hitting red five times in a row in American Roulette are 1:41 (or 2.38%). Those are the same odds as hitting black five times a row.

Relevant Resources